# 3.1 概率基础

## 如何理解概率？

上一章节我们学习了模型的基本概念，这一章我们开始学习概率推断。在理解概率之前，我们需要明确在使用“概率”这一术语时的一些基本概念。

### 实验（experiment）

实验是一个不能准确预测其结果的过程。简单地说，就是一个“你永远不知道会发生什么”的情景。想象一下，你拿起一个骰子，闭上眼睛，用力一甩，然后睁开眼睛看到结果。你无法准确地说出骰子会落在哪个数字上，这就是一个典型的实验。每次掷骰子，你都会得到一个不同的结果。

### 简单事件（simple event）

简单事件是实验的一个具体结果。在你扔出筛子后，睁眼看到骰子的最上面是“3”。简单事件之间是互斥的（mutually exclusive），即在一次实验中只能发生一个简单事件。但是，一组简单事件是完备的（collectively exhaustive），意味着至少有一个结果会发生。就像掷骰子，掷一次的结果至少为1-6的值，你看到的“3”就是本次的简单事件。这就像是你找对象，可能很多人都和你来电，但是最后你只能和其中一位终成眷属（互斥）！但无论如何，你终会找到属于你的那一位（完备）！

### 样本空间（sample space）

样本空间是一个实验中所有可能的结果的集合。例如你在掷一枚6个面的骰子的时候，样本空间是$${1, 2, 3, 4, 5, 6}$$。或者你去奶茶点奶茶，菜单上列出了所有的产品，这些产品组成了你点到的奶茶类型这件事的样本空间。

### 事件（event）

事件是样本空间的一个子集，可以包含一个或多个简单事件。例如你掷了三次骰子，其结果为奇数$${1, 3, 5}$$。在数学的形式化表示里，我们通常使用 $${}$$来表示一个集合（如样本空间和事件）。

当你正在学习的时候，你的朋友来找你，他想和你一起玩一个掷骰子的游戏，谁输了就要请今天下午的奶茶，你觉得这很公平。于是你拿了一枚质地均匀的六面骰子，你和你的朋友打算每人掷三次，最后计算掷出来的结果总和起来，谁的分数更小谁就负责请奶茶。你拿起骰子掷了三次，得到的结果是$${5, 6, 5}$$。你的朋友惊呆了，认为这个骰子有问题，强烈要求你证明这个筛子的每一面掷出的概率都是一样的。你感到十分的为难，继续翻书。

### 相对频率（relative frequency）

假设 $$N$$ 次实验中，事件 $$A$$ 实际出现了$$f$$ 次。比例 $$\frac{f}{N}$$  就是 $$N$$ 次实验中事件 $$A$$ 出现的相对频率。

### 概率（probability）

当 $$N$$  很小时，相对频率是不规则的。当 $$N$$ 很大时，相对频率会趋向稳定。其趋向的稳定值就是事件$$A$$ 的概率（probability）：

$$
p(A)=\lim\_{N\to\inf}\frac fN
$$

你向朋友解释道，虽然你这次掷出了较高的分数，但这并不意味着骰子有问题。要证明骰子是公平的，我们需要进行大量的实验，通过相对频率的方法来估计每个数字出现的概率。你和朋友决定掷骰子 1000 次，并记录每个数字出现的次数。朋友说你来掷骰子，他来计数。然后计算相对频率，并比较这些相对频率。如果每个数字的相对频率接近 ( 1/6 )，就可以证明骰子是公平的。

经过1000次掷骰子的实验，你们得到如下结果：

* 1 出现了 167 次
* 2 出现了 162 次
* 3 出现了 165 次
* 4 出现了 168 次
* 5 出现了 169 次
* 6 出现了 169 次

然后你们计算相对频率：

* 1 的相对频率： ( 167/1000 = 0.167 )
* 2 的相对频率： ( 162/1000 = 0.162 )
* 3 的相对频率： ( 165/1000 = 0.165 )
* 4 的相对频率： ( 168/1000 = 0.168 )
* 5 的相对频率： ( 169/1000 = 0.169 )
* 6 的相对频率： ( 169/1000 = 0.169 )

这些相对频率都接近 ( 1/6 )，说明骰子是公平的。你的朋友也开始掷他的三次，他得到的三次结果是$${3,4,1}$$，他大呼倒霉，但还是大方地拿出手机和你一点点上喜爱的奶茶（朋友说：你这个例子太扯了，当你说出要掷骰子1000次的时候，他已经让你开始选奶茶了）。

你喝着同学请的奶茶，想到是否能有数学方法来将以上过程简化，不用每次遇到此类事件都做上千次重复呢。在继续学习中，你发现，**随机变量**是一个将随机试验的每个可能结果映射到一个数值的函数。它的本质是将不确定性用数学方式表达出来。通过使用随机变量，我们可以用数学方式来处理这些不确定的事件。例如，在掷骰子的例子中，我们可以定义一个随机变量 $$X$$，其取值为骰子的面值。这样，我们就可以通过对有限次实验结果的记录来计算概率和其他统计量。

## 概率的不同类型

随机变量可以分类为以下三种类型：

* #### 布尔随机变量（Boolean random variable）

  只有两个可能值的随机变量（例如投硬币的正反面，或者有些事件的真和假）。
* 离散随机变量（Discrete random variable）

  有可数的有限个可能值的随机变量（例如骰子）。
* 连续随机变量（Continuous random variable）

  有不可数的无限个可能值的随机变量（例如身高、体重）。这些变量可以被数学化描述，通常使用概率质量函数（对于离散随机变量）或概率密度函数（对于连续随机变量）来表示。

### 概率空间（Probability space）

假定 ξ 是一个有限的简单事件集合，$$p$$ 是一个从 ξ 到非负实数的函数，且满足：

$$
\sum\_{e \in \xi} p(e) = 1
$$

这里 $$ξ$$ 是采样空间，$$p(e)$$ 是 $$e$$的概率，$$ξ, p$$ 组成了一个概率空间。

### 复合事件（Compound event）

一个采样空间里面的若干个事件组成了一个具有某种性质的复合事件（例如骰子中的奇数项）。复合事件可以看作是简单事件的集合，其概率可以通过对构成它的简单事件的概率求和得到。例如，对于骰子中的奇数事件，其概率为：

$$P(\text{奇数}) = P(1) + P(3) + P(5)$$

在公平的骰子中，这个概率等于 $$1/2$$。通过这种方式，我们可以使用概率空间的定义来计算更复杂的事件的概率，从而对随机现象进行量化分析。

### 概率的三种主要类型

1. 联合概率（Joint probability）
2. 条件概率（Conditional probability）
3. 边缘概率（Marginal probability）

联合概率（Joint probability）

**定义**：联合概率是指多个随机事件同时发生的概率。

**特征**：

* 涉及两个或多个随机变量
* 描述这些随机变量同时取特定值的概率
* 适用于离散和连续随机变量，但表示方式可能不同

**形式化表示：**对于离散随机变量 X 和 Y，其联合概率可表示为： $$P(X=x, Y=y)$$

**例如：** $$P(\text{蛀牙 = true}, \text{牙痛 = true}, \text{天气 = 下雪}) = 0.2$$， 这表示蛀牙、牙痛和下雪这三个事件同时发生的概率为0.2。

**注意：**对于离散随机变量，联合概率可以用概率质量函数（PMF）表示；对于连续随机变量，联合概率通过联合概率密度函数（PDF）定义。

#### 条件概率（Conditional probability）

**定义**：条件概率是指在已知一个事件发生的条件下，另一个事件发生的概率。

**形式化表示**：事件 A 在事件 B 已发生的条件下发生的概率表示为： $$P(A|B) = \frac{P(A \cap B)}{P(B)}, \quad P(B) > 0$$

**例如：**考虑一个袋子里有 3 个红球和 2 个蓝球。我们随机抽取一个球，然后不放回，再抽取第二个球。

事件 A：第二个抽到的是红球。\
事件 B：第一个抽到的是红球。

我们需要计算在第一个抽到红球的情况下，第二个抽到红球的概率。

1. 首先计算事件 B 发生的概率，即第一个抽到红球的概率: $$P(B) = \dfrac{3}{5}$$
2. 首先计算事件 B 发生的概率，即第一个抽到红球的概率: $$P(B) = \dfrac{3}{5}$$
3. 接着，我们计算在第一个抽到红球的情况下，第二个抽到红球的概率: 在第一个红球被抽走后，袋子里剩下 2 个红球和 2 个蓝球，因此第二个抽到红球的概率为: $$P(A|B) = \dfrac{2}{4} = \dfrac{1}{2}$$
4. 最后，我们可以验证条件概率公式: $$P(A \cap B) = \dfrac{3}{5} \times \dfrac{2}{4} = \dfrac{3}{5} \times \dfrac{1}{2} = \dfrac{3}{10}$$ $$P(A|B) = \dfrac{P(A \cap B)}{P(B)} = \dfrac{\dfrac{3}{10}}{\dfrac{3}{5}} = \dfrac{3}{10} \times \dfrac{5}{3} = \dfrac{1}{2}$$

#### 边缘概率（Marginal probability）

**定义：**边缘概率 $$P(A)$$ 是指单个事件$$A$$ 发生的概率，而不考虑其他事件的情况。边缘概率可以通过联合概率分布来计算。

**计算方法：**对于离散随机变量，通过求和得到；对于连续随机变量，通过积分得到。

**形式化表示：**假定一个联合分布 $$P(A, B)$$，我们可以通过对所有 $$B$$ 的值求和来得到 $$P(A)$$     $$P(A) = \sum\_{B} P(A|B) \cdot P(B) \quad \quad (1)$$

公式$$(1)$$表示边缘概率 $$P(A)$$ 是通过条件概率 $$P(A|B)$$乘以 $$P(B)$$ 后，对所有可能的 $$B$$ 进行求和得到的。

#### 条件概率与独立性

我们一定有: $$P(A \cap B) = P(A|B) \cdot P(B) \quad \text{(2)}$$

但是不一定有： $$P(A \cap B) = P(A) \cdot P(B) \quad \text{(3)}$$

公式 $$3$$ 当且仅当 A 和 B 独立的时候才成立。

#### 概率独立性

当两个随机变量独立时，其充要条件是： $$P(A, B) = P(A) \cdot P(B) \quad \text{(4)}$$

注意，如果有： $$P(A, B|C) = P(A|C) \cdot P(B|C) \quad \text{(5)}$$

并不能一定推出公式$$(4)$$，公式$$(5)$$ 成立只意味着$$A$$ 和 $$B$$ 在已知 $$C$$的条件下独立，不能说$$A$$和$$B$$独立。

假设我们有以下联合分布：

| A\B | B1  | B2  |
| --- | --- | --- |
| A1  | 0.1 | 0.2 |
| A2  | 0.3 | 0.4 |

在这个联合分布中，$$P(A = A1, B = B1) = 0.1 ， P(A = A1, B = B2) = 0.2 ，P(A = A2, B = B1) = 0.3 ， P(A = A2, B = B2) = 0.4$$

我们想要计算边缘概率 $$P(A = A1)$$，可以通过对所有 $$B$$ 的可能值求和来实现： $$P(A = A1) = P(A = A1, B = B1) + P(A = A1, B = B2) = 0.1 + 0.2 = 0.3 \quad \text{(6)}$$

同样地，边缘概率 $$P(A = A2)$$ 为： $$P(A = A2) = P(A = A2, B = B1) + P(A = A2, B = B2) = 0.3 + 0.4 = 0.7 \quad \text{(7)}$$

通过这个例子，可以清晰地看到如何通过联合概率来计算边缘概率。这个过程本质上是对联合分布中的某一个维度进行“投影”，得到单个事件的概率分布。

总结来说，联合概率与边缘概率的关系可以帮助我们更好地理解和计算复杂事件的概率分布。

## 概率的数学模型

在理解了概率的不同类型后，我们需要理解如何使用数学模型来描述不同的概率类型。

### 概率质量函数（Probability Mass Function）

#### 定义

概率质量函数（PMF）是一个离散随机变量的概率分布，它描述了随机变量在每一个特定取值上的概率。对于每一个可能的取值，PMF 给出了该值出现的概率。

#### 公式

设离散随机变量 $$X$$ 的可能取值为 $$(x\_1, x\_2, ..., x\_n)$$，概率质量函数 $$P(X = x\_i) = p\_i$$，满足以下条件：

$$
\sum\_{i=1}^{n} p\_i = 1 \quad \text{and} \quad 0 \leq p\_i \leq 1 \quad \forall i
$$

假如我们有一个骰子，骰子的六个面分别有 1 到 6 的点数，骰子每个面朝上的概率相等。则 PMF 为：

$$
P(X = x) = \dfrac{1}{6} \quad \text{for} \quad x \in {1, 2, 3, 4, 5, 6}
$$

### 概率密度函数（Probability Density Function）

#### 定义

概率密度函数（PDF）是一个连续随机变量的概率分布，它描述了随机变量在某个确定的取值点附近的可能性密度。PDF 本身的值并不是概率，但通过积分可以得到某一区间内的概率。

#### 公式

设连续随机变量 $$X$$ 的概率密度函数为 $$f(x)$$，则 $$X$$ 在区间 $$\[a, b]$$上的概率为：

$$
P(a \leq X \leq b) = \int\_{a}^{b} f(x) , dx
$$

例如下图中蓝色区域区间的概率：

![](https://markdown.liuchengtu.com/work/uploads/upload_d8737a294387a7b4d0c392d145c8a5a7.png)

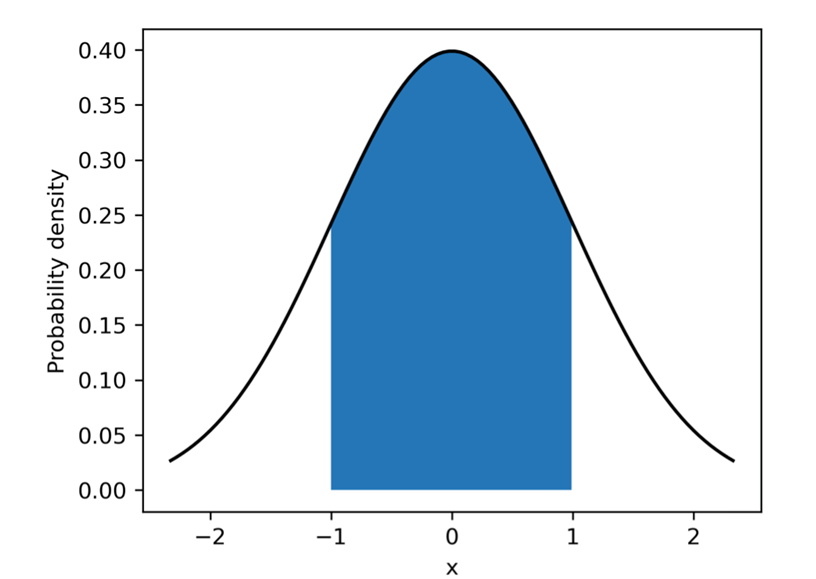
**例如正态分布，概率密度函数为：**

$$
f(x) = \dfrac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\dfrac{(x - \mu)^2}{2\sigma^2} \right)
$$

其中，$$\mu$$是均值， $$\sigma$$是标准差。

### 累积分布函数（Cumulative Distribution Function）

#### 定义

累积分布函数 CDF 是用来计算随机变量小于或等于某个特定值的概率。对于离散和连续随机变量都适用。CDF 可以通过积分（对于 PDF）或求和（对于 PMF）得到。

#### 公式

对于离散随机变量 $$X$$：

$$
F(x) = P(X \leq x) = \sum\_{x\_i \leq x} P(X = x\_i)
$$

对于连续随机变量 $$X$$：

$$
F(x) = P(X \leq x) = \int\_{-\infty}^{x} f(t) , dt
$$

在实际应用中，我们面对不同类型的随机变量时，会使用不同的概率分布。此处我们介绍最常用的两个概率分布以及它们在 Python 代码中的使用示例。

**首先是离散变量中的布尔随机变量，使用伯努利分布（Bernoulli Distribution）来描述。**

#### 伯努利分布

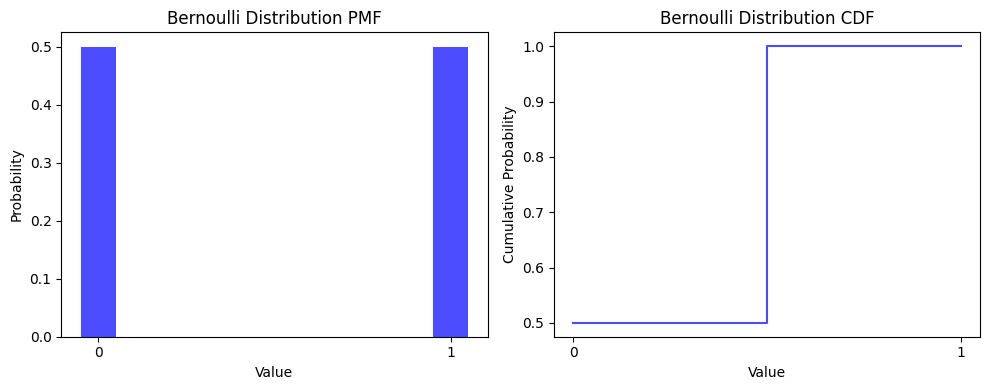
伯努利分布是一种离散分布，用来描述只有两种可能结果的随机试验。例如，抛硬币的结果（正面或反面）就可以用伯努利分布来描述。伯努利分布的概率质量函数为：

$$
P(X = x) = p^x (1 - p)^{1 - x} \quad \text{for} \quad x \in {0, 1}
$$

其中，$$p$$ 是事件发生的概率（如硬币正面朝上的概率）。

**Python 实现示例**

使用 Python 中的 `scipy.stats` 模块可以很方便地进行伯努利分布的计算和采样。

```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
# 定义伯努利分布的参数
p = 0.5 # 事件发生的概率
# 生成伯努利分布的随机样本
sample_size = 1000
samples = bernoulli.rvs(p, size=sample_size)
# 计算概率质量函数（PMF）
pmf = bernoulli.pmf([0, 1], p)
# 计算累积分布函数（CDF）
cdf = bernoulli.cdf([0, 1], p)
print("PMF:", pmf)
print("CDF:", cdf)
# 绘制概率质量函数（PMF）
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.bar([0, 1], pmf, width=0.1, color='blue', alpha=0.7)
plt.xticks([0, 1])
plt.xlabel('Value')
plt.ylabel('Probability')
plt.title('Bernoulli Distribution PMF')

# 绘制累积分布函数（CDF）
plt.subplot(1, 2, 2)
plt.step([0, 1], cdf, where='mid', color='blue', alpha=0.7)
plt.xticks([0, 1])
plt.xlabel('Value')
plt.ylabel('Cumulative Probability')
plt.title('Bernoulli Distribution CDF')
```

![](https://markdown.liuchengtu.com/work/uploads/upload_16f45a83f508bb525a7ed5780fe0a00d.png)

```python
# 绘制采样结果的直方图
plt.hist(samples, bins=2, edgecolor='black', density=True)
plt.xticks([0, 1])
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.title('Bernoulli Distribution Sampling')
plt.show()
```

![](https://markdown.liuchengtu.com/work/uploads/upload_2ce5607fe14120b5d369221e420a13a3.png)

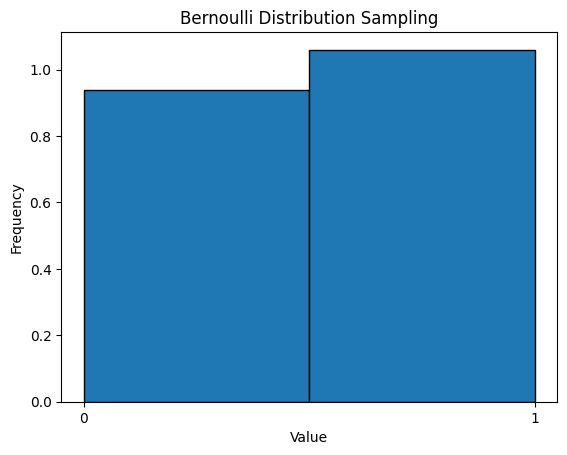
**其次是连续变量中的正态随机变量，使用正态分布（Normal Distribution）来描述。**

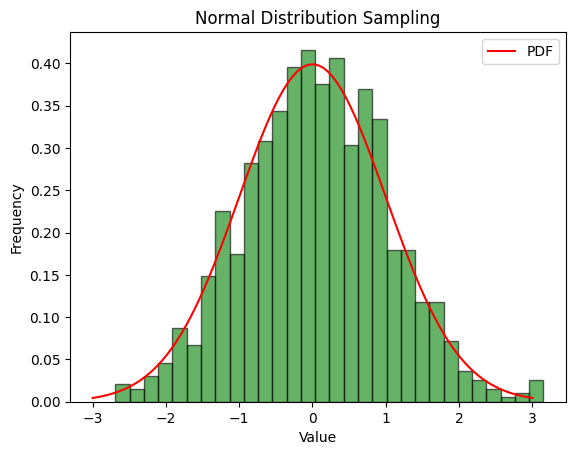
#### 正态分布

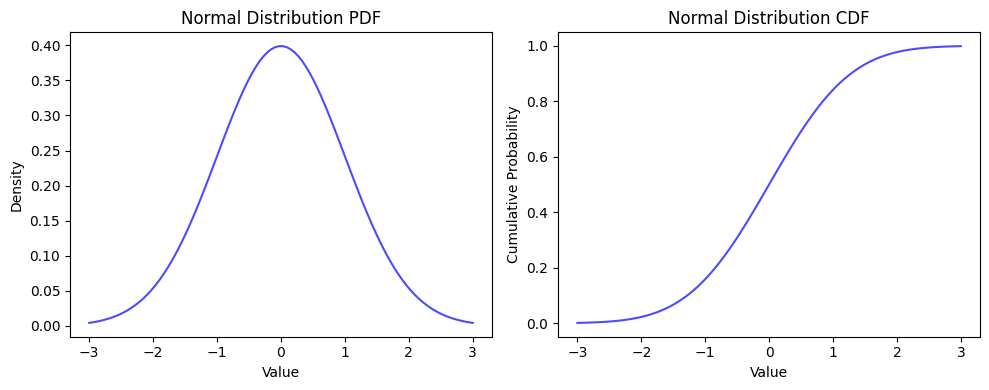
正态分布是最常见的连续概率分布之一，广泛应用于自然和社会科学中。例如，人的身高和体重都可以用正态分布来描述。正态分布的概率密度函数为：

$$
f(x) = \dfrac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\dfrac{(x - \mu)^2}{2\sigma^2} \right)
$$

其中，$$\mu$$ 是均值，$$\sigma$$ 是标准差。

**Python 实现示例**

使用 Python 中的 `scipy.stats` 模块可以很方便地进行正态分布的计算和采样。

```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# 定义正态分布的参数
mu = 0  # 均值
sigma = 1  # 标准差

# 生成正态分布的随机样本
sample_size = 1000
samples = norm.rvs(mu, sigma, size=sample_size)

# 计算概率密度函数（PDF）
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
pdf = norm.pdf(x, mu, sigma)

# 计算累积分布函数（CDF）
cdf = norm.cdf(x, mu, sigma)

# 打印 PDF 和 CDF 值
print("PDF:", pdf)
print("CDF:", cdf)

# 绘制概率密度函数（PDF）
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(x, pdf, label='PDF', color='blue', alpha=0.7)
plt.xlabel('Value')
plt.ylabel('Density')
plt.title('Normal Distribution PDF')

# 绘制累积分布函数（CDF）
plt.subplot(1, 2, 2)
plt.plot(x, cdf, label='CDF', color='blue', alpha=0.7)
plt.xlabel('Value')
plt.ylabel('Cumulative Probability')
plt.title('Normal Distribution CDF')

# 调整子图布局
plt.tight_layout()
plt.show()
```

![](https://markdown.liuchengtu.com/work/uploads/upload_5b43ebacde2d4ef15d80514d778495c2.png)

```python
# 绘制采样结果的直方图
plt.hist(samples, bins=30, edgecolor='black', density=True, alpha=0.6, color='g')
plt.plot(x, pdf, 'r', label='PDF')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.title('Normal Distribution Sampling')
plt.legend()
plt.show()
```

![](https://markdown.liuchengtu.com/work/uploads/upload_0b444c646b556830693aabbaf70db46b.png)

#### 多项分布

多项分布是一种离散分布，是两个事件的二项分布的多项推广。它描述了在一次试验中，多个可能的离散结果的发生次数。

**Python 实现示例**

使用 `numpy` 可以方便地进行多项分布的计算和采样。

```python
import numpy as np

# 定义多项分布的参数
n = 10  # 试验次数
p = [0.2, 0.5, 0.3]  # 每个事件发生的概率

# 生成多项分布的随机样本
samples = np.random.multinomial(n, p, size=1000)
```

#### Beta 分布

Beta 分布是一种连续分布，定义在 $$(0, 1)$$ 上，通常作为伯努利分布的先验分布。

Beta 分布的概率密度函数为：

$$
f(x; \alpha, \beta) = \dfrac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}
$$

其中，$$\alpha$$ 和 $$\beta$$ 是形状参数，$$B(\alpha,\beta)$$ 是 Beta 函数。

**Python 实现示例**

使用 `scipy.stats` 可以很方便地进行 Beta 分布的计算和采样。

```python
from scipy.stats import beta

# 定义 Beta 分布的参数
alpha, beta_param = 2, 5

# 生成 Beta 分布的随机样本
samples = beta.rvs(alpha, beta_param, size=1000)

```

#### Dirichlet 分布

Dirichlet 分布是一种连续分布，是 Beta 分布在高维（例如，掷骰子）的推广。Dirichlet 分布通常用于多项分布参数的先验分布。

**Python 实现示例**

使用 `numpy` 可以方便地进行 Dirichlet 分布的计算和采样。

```python
import numpy as np
# 定义 Dirichlet 分布的参数
alpha = [1, 2, 3]
# 生成 Dirichlet 分布的随机样本
samples = np.random.dirichlet(alpha, size=1000)
```

#### 均匀分布

均匀分布是一种连续分布，在区间 $$\[a, b]$$ 上的所有值出现的概率相等。均匀分布的概率密度函数为：

$$
f(x) = \begin{cases} \dfrac{1}{b-a} & a \leq x \leq b \ 0 & \text{otherwise} \end{cases}
$$

**Python 实现示例**

使用 `scipy.stats` 可以很方便地进行均匀分布的计算和采样。

```python
from scipy.stats import uniform

# 定义均匀分布的参数
a = 0  # 下限
b = 1  # 上限

# 生成均匀分布的随机样本
sample_size = 1000
samples = uniform.rvs(a, b-a, size=sample_size)
```

### 对分布的特征描述

在概率论和统计学中，描述分布特征的常用指标包括**中位数**、**期望（均值）**和**方差**等。这些指标帮助我们理解数据的中心趋势和离散程度。

**中位数**是数据集中居中的值，即把所有数据按大小顺序排列后处于中间位置的值。对于偶数个数据，中位数是中间两个数的平均值**。**

* **伯努利分布**：对于参数 $$p$$ 的伯努利分布，如果 $$p \leq 0.5$$, 中位数为 $$0$$，否则为 $$1$$。
* **正态分布**：正态分布的中位数等于其均值 $$\mu$$。

**期望**是随机变量所有可能取值的加权平均数，其中，权重为各取值的概率**。**

* **伯努利分布**：对于参数 $$p$$ 的伯努利分布，期望为 $$p$$。

$$
E(X) = p
$$

* **正态分布**：对于均值 $$\mu$$ 和标准差 $$\sigma$$ 的正态分布，期望为 $$\mu$$。

$$
E(X) = \mu
$$

**方差**是度量随机变量取值与其期望之间偏离程度的非负值**。**

* **伯努利分布**：对于参数 $$p$$ 的伯努利分布，方差为 $$p(1 - p)$$。

$$
\text{Var}(X) = p(1 - p)
$$

* **正态分布**：对于均值 $$\mu$$ 和标准差 $$\sigma$$ 的正态分布，方差为 $$\sigma^2$$。

$$
\text{Var}(X) = \sigma^2
$$

以下给出计算一些常见分布的python 示例

```python
import numpy as np
from scipy.stats import bernoulli
# 定义伯努利分布的参数
p = 0.5
# 计算伯努利分布的期望和方差
mean = bernoulli.mean(p)
var = bernoulli.var(p)
print("Bernoulli Distribution - Mean:", mean)
print("Bernoulli Distribution - Variance:", var)
import numpy as np
from scipy.stats import norm

# 定义正态分布的参数
mu = 0  # 均值
sigma = 1  # 标准差

# 计算正态分布的期望和方差
mean = norm.mean(loc=mu, scale=sigma)
var = norm.var(loc=mu, scale=sigma)

print("Normal Distribution - Mean:", mean)
print("Normal Distribution - Variance:", var)
```